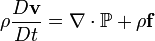General form of the equation
The general form of the Navier–Stokes equations for the conservation of momentum is: is the fluid density,
is the fluid density, is the substantive derivatives (also called the material derivative).
is the substantive derivatives (also called the material derivative). is the velocity vector,
is the velocity vector,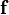 is the body force vector, and
is the body force vector, and is a tensor that represents the surface forces applied on a fluid particle (the stress tensor).
is a tensor that represents the surface forces applied on a fluid particle (the stress tensor).
 is a symmetric tensor. In general, (in three dimensions)
is a symmetric tensor. In general, (in three dimensions)  has the form:
has the form: are normal stresses,
are normal stresses, are tangential stresses (shear stresses).
are tangential stresses (shear stresses).
.....